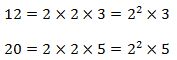Menghitung FPB dan KPK dengan Pohon Faktor

       Faktor Persekutuan Terbesar (FPB) adalah suatu faktor dari dua atau lebih bilangan yang memiliki nilai terbesar, sedangkan Kelipatan Persekutuan Terkecil (KPK) adalah kelipatan dari dua atau lebih bilangan yang memiliki nilai terkecil. Ada beberapa cara yang digunakan untuk menghitung FPB dan KPK salah satunya adalah menggunakan pohon faktor. Pohon faktor diawali dengan menentukan faktorisasi prima dari suatu bilangan. Faktorisasi prima adalah perkalian antar bilangan prima yang membentuk bilangan yang dimaksud.

       Konsep yang perlu diperhatikan saat menentukan FPB dan KPK adalah cara pemilihan angka yang tepat setelah faktorisasi prima diperoleh. Cara untuk menentukan FPB ialah dengan memperhatikan angka yang sama pada faktorisasi bilangan-bilangan tersebut, kemudian, pilihah yang berpangkat paling kecil. Apabila terdapat dua atau lebih angka yang bernilai sama, maka gandakanlah angka-angka tersebut. Sedangkan, untuk menentukan KPK dengan cara memilih pangkat tertinggi untuk angka yang sama dan menggandakannya dengan angka-angka yang tidak sama yang ada pada faktorisasi prima. Untuk lebih jelasnya dibahas pada contoh soal berikut

Contoh 1:

Tentukan FPB dan KPK dari 12 dan 20

Faktorisasi prima dari

Pada Contoh 1 terlihat angka yang sama pada faktorisasi prima adalah 2², tidak ada pangkat tertinggi dan terendah. Sehingga dapat digunakan pada FPB dan KPK. Selain itu, terdapat angka tidak sama antara kedua faktorisasi yaitu 3 dan 5. Berdasarkan penjelasan di atas, diperoleh FPB dan KPK dari 12 dan 20 adalah

FPB = 2² = 4 dan

KPK = 2² x 3 x 5 = 60.

Contoh 2:

Tentukan FPB dan KPK dari 12, 20, dan 28!

Faktorisasi prima dari

Pada Contoh 2 terlihat angka yang sama pada faktorisasi prima adalah 2², tidak ada pangkat tertinggi dan terendah. Sehingga dapat digunakan pada FPB dan KPK. Selain itu, terdapat angka tidak sama antara ketiga faktorisasi yaitu 3, 5, dan 7. Berdasarkan penjelasan di atas, diperoleh FPB dan KPK dari 12, 20, dan 28 adalah

FPB = 2² = 4 dan

KPK = 2² x 3 x 5 x 7 = 420.

Selamat Belajar J

Cara Mudah Menyelesaikan Soal Cerita dengan Diagram Venn

Biasanya beberapa siswa mengalami kesulitan dalam menyelesaikan soal cerita tentang himpunan. Sebenarnya, untuk menyelesaikan masalah tersebut terdapat beberapa cara, salah satunya menggunakan diagram Venn. Kali ini saya akan membahas tentang beberapa contoh soal yang diselesaikan menggunakan diagram Venn.

Contoh 1:

Apabila di dalam suatu kelas yang terdiri dari 40 siswa terdapat 25 anak gemar bermain sepak bola dan 18 anak gemar berenang. Apabila terdapat 8 anak gemar keduanya, berapa banyak anak yang tidak gemar keduanya?

Penyelesaian:       

Gambarlah diagram Venn sesuai dengan Contoh 1.

Berdasarkan diagram Venn di samping terlihat bahwa

Jumlah siswa yang menyukai sepak bola tapi tidak suka renang sebanyak 25 – 8 = 17 anak.

Jumlah siswa yang menyukai renang tapi tidak suka sepak bola sebanyak 18 – 8 = 10 anak.

Jadi, siswa yang tidak senang keduanya adalah 40 – (17 + 8 + 10) = 40 -35 =5 anak.

Contoh 2:

Pada hari Jumat dilakukan survey kepada 30 orang dewasa tentang mata pelajaran favorit saat masih bersekolah. 12 orang menyukai pelajaran IPA, 20 orang menyukai matematika, 3 orang tidak menyukai keduanya, dan yang lainnya menyatakan menyukai pelajaran IPA dan Matematika. Berapa banyak orang yang suka kedua mata pelajaran?

Penyelesaian:  

Gambarlah diagram Venn sesuai dengan Contoh 2.

Pertama, misalkan banyak orang yang menyukai keduanya dengan x, sehingga banyak orang yang menyukai IPA, tidak menyukai matematika sebanyak 12 – x dan banyak orang yang menyukai matematika, tidak menyukai IPA sebanyak 20 –x. Maka

30 = 12 – x + x + 20 – x +3

30 = -x + 35

x = 35 – 30

x = 5 orang

Jadi banyak orang yang menyukai IPA dan matematika saat masih bersekolah adalah 5 orang.

Selamat Belajar. J

Mencari Keliling dan Luas Bangun Datar Gabungan

Pada dasarnya untuk mencari keliling dan luas bangun datar gabungan itu sama halnya mencari keliling dan luas sebuah bangun datar. Hanya perlu pemahaman sedikit konsep tentang keliling dan luas. Berikut dibahas mengenai keliling dan luas lebih lanjut.

1.        Keliling Bangun Datar Gabungan

Seperti yang disebutkan di atas, bahwa untuk mencari keliling bangun datar gabungan sama halnya dengan mencari keliling sebuah bangun datar. Sebelumnya, perlu dipahami apa yang dimaksud dengan keliling. Coba bayangkan, apabila kita berlari mengelilingi sebuah lapangan sebanyak satu putaran berawal dari titik A dan berakhir di titik A pula. Lalu, kita ditanya, “Berapa meter kah kamu berlari tadi?”. Tentunya kamu akan menjumlahkan panjang setiap sisi yang telah kamu lalui. Yah, itulah keliling. Keliling adalah hasil penjumlahan dari sisi-sisi yang mengelilingi suatu bangun.

Coba perhatikan contoh bangun gabungan di bawah ini!

Pada gambar di samping terlihat bahwa keliling bangun gabungan tersebut ditandai dengan garis berwarna hijau. Sedangkan garis hitam ditengah bukan merupakan keliling bangun gabungan tersebut karena garis itu bukan merupakan sisi bagian tepi bangun gabungan. Tampak bahwa garis hijau terdiri dari dua buah panjang dan sebuah lebar dari persegi panjang serta bangun setengah lingkaran yang diameternya sama dengan lebar persegi panjang (l=d). Maka dari itu, keliling bangun gabungan di samping ialah 

2.        Luas Bangun Datar Gabungan

Sama halnya dengan keliling, luas bangun datar gabungan juga sama dengan luas suatu bangun datar. Namun yang perlu diperhatikan kapan luas masing-masing bangun pada bangun gabungan dijumlah dan kapan dikurangi. Perhatikan contoh berikut ini.

Terlihat pada gambar bahwa bangun memiliki dua bangun yaitu persegi panjang dan setengah lingkaran. Untuk menghitung luas dari bangun gabungan tersebut hanya perlu menjumlahkan luas masing-masing bangun datar pada bangun gabungan tersebut. Jadi, pada gambar dihitung luas persegi panjang pxl dan luas setengah lingkaran 1/2 phi r^2 , kemudian dijumlahkan.

       Sebagai contoh bangun gabungan yang diselesaikan dengan cara dikurangi, adalah sebagai berikut

Gambar di samping terdiri dari dua bangun datar yaitu persegi dan lingkaran. Lingkaran berhimpit dengan persegi dengan diameter lingkaran sama dengan sisi persegi. Kita diminta untuk menentukan luas daerah yang berwarna merah. Bayangkan kita mempunyai kertas berbentuk persegi ditenahnya kita membuat arsiran berbentuk lingkaran ditengahnya yang besarnya hampir sama dengan kertas. Kemudian kita menggunting arsiran tersebut dan membuangnya. Tersisa bagian tepinya. Untuk menghitung luas sisa kertas tersebut tentu kita akan menghitung luas kertas tersebut kemudian menguranginya dengan luas arsiran lingkaran bukan? Benar sekali, untuk menghitung luas daerah warna merah pada gambar dengan mudah kita harus mengurangi luas persegi dengan luas lingkaran, sehingga luas bangun gabungan di atas adalah